`sklearn.mixture`.GaussianMixture¶

class sklearn.mixture.GaussianMixture(n_components=1, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)[source]¶

Gaussian Mixture.

Representation of a Gaussian mixture model probability distribution. This class allows to estimate the parameters of a Gaussian mixture distribution.

New in version 0.18.

GaussianMixture.

Read more in the User Guide.

Parameters:

n_components : int, defaults to 1.

The number of mixture components.

covariance_type : {‘full’, ‘tied’, ‘diag’, ‘spherical’},

defaults to ‘full’.

String describing the type of covariance parameters to use. Must be one of:

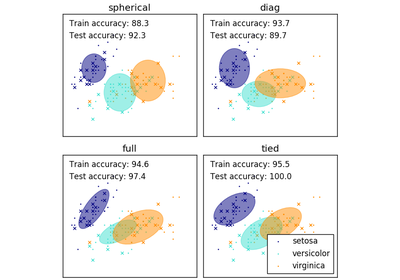
'full' (each component has its own general covariance matrix),
'tied' (all components share the same general covariance matrix),
'diag' (each component has its own diagonal covariance matrix),
'spherical' (each component has its own single variance).

tol : float, defaults to 1e-3.

The convergence threshold. EM iterations will stop when the lower bound average gain is below this threshold.

reg_covar : float, defaults to 0.

Non-negative regularization added to the diagonal of covariance. Allows to assure that the covariance matrices are all positive.

max_iter : int, defaults to 100.

The number of EM iterations to perform.

n_init : int, defaults to 1.

The number of initializations to perform. The best results are kept.

init_params : {‘kmeans’, ‘random’}, defaults to ‘kmeans’.

The method used to initialize the weights, the means and the precisions. Must be one of:
'kmeans' : responsibilities are initialized using kmeans.
'random' : responsibilities are initialized randomly.

weights_init : array-like, shape (n_components, ), optional

The user-provided initial weights, defaults to None. If it None, weights are initialized using the init_params method.

means_init: array-like, shape (n_components, n_features), optional :

The user-provided initial means, defaults to None, If it None, means are initialized using the init_params method.

precisions_init: array-like, optional. :

The user-provided initial precisions (inverse of the covariance matrices), defaults to None. If it None, precisions are initialized using the ‘init_params’ method. The shape depends on ‘covariance_type’:
(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

random_state : RandomState or an int seed, defaults to None.

A random number generator instance.

warm_start : bool, default to False.

If ‘warm_start’ is True, the solution of the last fitting is used as initialization for the next call of fit(). This can speed up convergence when fit is called several time on similar problems.

verbose : int, default to 0.

Enable verbose output. If 1 then it prints the current initialization and each iteration step. If greater than 1 then it prints also the log probability and the time needed for each step.

verbose_interval : int, default to 10.

Number of iteration done before the next print.

Attributes:

weights_ : array-like, shape (n_components,)

The weights of each mixture components.

means_ : array-like, shape (n_components, n_features)

The mean of each mixture component.

covariances_ : array-like

The covariance of each mixture component. The shape depends on covariance_type:

(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

precisions_ : array-like

The precision matrices for each component in the mixture. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on covariance_type:
(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

precisions_cholesky_ : array-like

The cholesky decomposition of the precision matrices of each mixture component. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on covariance_type:
(n_components,)                        if 'spherical',
(n_features, n_features)               if 'tied',
(n_components, n_features)             if 'diag',
(n_components, n_features, n_features) if 'full'

converged_ : bool

True when convergence was reached in fit(), False otherwise.

n_iter_ : int

Number of step used by the best fit of EM to reach the convergence.

lower_bound_ : float

Log-likelihood of the best fit of EM.

See also

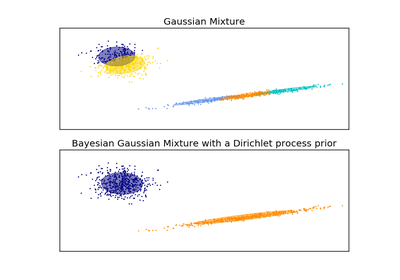
BayesianGaussianMixture: Gaussian mixture model fit with a variational inference.

Methods

`aic`(X)	Akaike information criterion for the current model on the input X.
`bic`(X)	Bayesian information criterion for the current model on the input X.
`fit`(X[, y])	Estimate model parameters with the EM algorithm.
`get_params`([deep])	Get parameters for this estimator.
`predict`(X[, y])	Predict the labels for the data samples in X using trained model.
`predict_proba`(X)	Predict posterior probability of data per each component.
`sample`([n_samples])	Generate random samples from the fitted Gaussian distribution.
`score`(X[, y])	Compute the per-sample average log-likelihood of the given data X.
`score_samples`(X)	Compute the weighted log probabilities for each sample.
`set_params`(\\params)	Set the parameters of this estimator.

__init__(n_components=1, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)[source]¶

aic(X)[source]¶

Akaike information criterion for the current model on the input X.

Parameters:

X : array of shape (n_samples, n_dimensions)

Returns:

aic: float :

The lower the better.

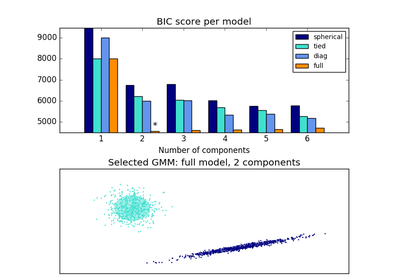
bic(X)[source]¶

Bayesian information criterion for the current model on the input X.

Parameters:

X : array of shape (n_samples, n_dimensions)

Returns:

bic: float :

The lower the better.

fit(X, y=None)[source]¶

Estimate model parameters with the EM algorithm.

The method fit the model n_init times and set the parameters with which the model has the largest likelihood or lower bound. Within each trial, the method iterates between E-step and M-step for max_iter times until the change of likelihood or lower bound is less than tol, otherwise, a ConvergenceWarning is raised.

Parameters:

X : array-like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

self :

get_params(deep=True)[source]¶

Get parameters for this estimator.

Parameters:

deep : boolean, optional

If True, will return the parameters for this estimator and contained subobjects that are estimators.

Returns:

params : mapping of string to any

Parameter names mapped to their values.

predict(X, y=None)[source]¶

Predict the labels for the data samples in X using trained model.

Parameters:

X : array-like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

labels : array, shape (n_samples,)

Component labels.

predict_proba(X)[source]¶

Predict posterior probability of data per each component.

Parameters:

X : array-like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

resp : array, shape (n_samples, n_components)

Returns the probability of the sample for each Gaussian (state) in the model.

sample(n_samples=1)[source]¶

Generate random samples from the fitted Gaussian distribution.

Parameters:

n_samples : int, optional

Number of samples to generate. Defaults to 1.

Returns:

X : array, shape (n_samples, n_features)

Randomly generated sample

y : array, shape (nsamples,)

Component labels

score(X, y=None)[source]¶

Compute the per-sample average log-likelihood of the given data X.

Parameters:

X : array-like, shape (n_samples, n_dimensions)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

log_likelihood : float

Log likelihood of the Gaussian mixture given X.

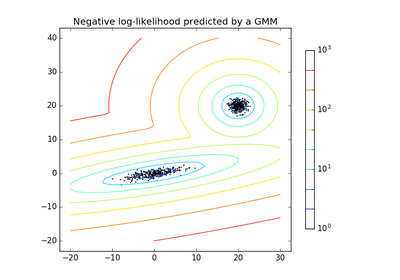
score_samples(X)[source]¶

Compute the weighted log probabilities for each sample.

Parameters:

X : array-like, shape (n_samples, n_features)

List of n_features-dimensional data points. Each row corresponds to a single data point.

Returns:

log_prob : array, shape (n_samples,)

Log probabilities of each data point in X.

set_params(**params)[source]¶

Set the parameters of this estimator.

The method works on simple estimators as well as on nested objects (such as pipelines). The latter have parameters of the form <component>__<parameter> so that it’s possible to update each component of a nested object.