Annotation

Table of Contents

• Annotation
  • Basic annotation
  • Advanced Annotation
    • Annotating with Text with Box
    • Annotating with Arrow
    • Placing Artist at the anchored location of the Axes
    • Using Complex Coordinates with Annotations
    • Using ConnectorPatch
    • Zoom effect between Axes
    • Define Custom BoxStyle

Basic annotation

The uses of the basic text() will place text at an arbitrary position on the Axes. A common use case of text is to annotate some feature of the plot, and the annotate() method provides helper functionality to make annotations easy. In an annotation, there are two points to consider: the location being annotated represented by the argument xy and the location of the text xytext. Both of these arguments are (x,y) tuples.

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111)

t = np.arange(0.0, 5.0, 0.01)
s = np.cos(2*np.pi*t)
line, = ax.plot(t, s, lw=2)

ax.annotate('local max', xy=(2, 1), xytext=(3, 1.5),
            arrowprops=dict(facecolor='black', shrink=0.05),
            )

ax.set_ylim(-2,2)
plt.show()

(Source code, png, pdf)

In this example, both the xy (arrow tip) and xytext locations (text location) are in data coordinates. There are a variety of other coordinate systems one can choose – you can specify the coordinate system of xy and xytext with one of the following strings for xycoords and textcoords (default is ‘data’)

argument	coordinate system
‘figure points’	points from the lower left corner of the figure
‘figure pixels’	pixels from the lower left corner of the figure
‘figure fraction’	0,0 is lower left of figure and 1,1 is upper right
‘axes points’	points from lower left corner of axes
‘axes pixels’	pixels from lower left corner of axes
‘axes fraction’	0,0 is lower left of axes and 1,1 is upper right
‘data’	use the axes data coordinate system

For example to place the text coordinates in fractional axes coordinates, one could do:

ax.annotate('local max', xy=(3, 1),  xycoords='data',
            xytext=(0.8, 0.95), textcoords='axes fraction',
            arrowprops=dict(facecolor='black', shrink=0.05),
            horizontalalignment='right', verticalalignment='top',
            )

For physical coordinate systems (points or pixels) the origin is the bottom-left of the figure or axes.

Optionally, you can enable drawing of an arrow from the text to the annotated point by giving a dictionary of arrow properties in the optional keyword argument arrowprops.

arrowprops key	description
width	the width of the arrow in points
frac	the fraction of the arrow length occupied by the head
headwidth	the width of the base of the arrow head in points
shrink	move the tip and base some percent away from the annotated point and text
**kwargs	any key for matplotlib.patches.Polygon, e.g., facecolor

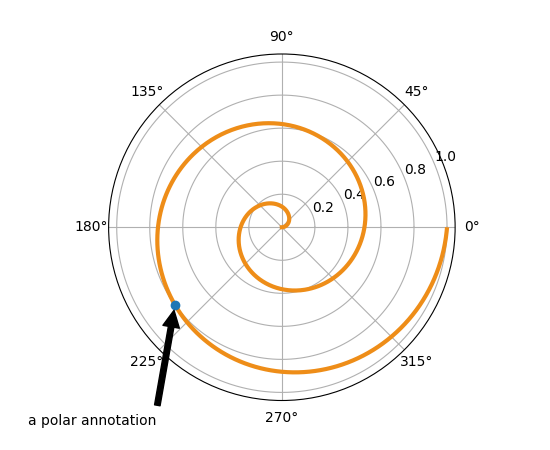
In the example below, the xy point is in native coordinates (xycoords defaults to ‘data’). For a polar axes, this is in (theta, radius) space. The text in this example is placed in the fractional figure coordinate system. matplotlib.text.Text keyword args like horizontalalignment, verticalalignment and fontsize are passed from annotate to the Text instance.

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111, polar=True)
r = np.arange(0,1,0.001)
theta = 2*2*np.pi*r
line, = ax.plot(theta, r, color='#ee8d18', lw=3)

ind = 800
thisr, thistheta = r[ind], theta[ind]
ax.plot([thistheta], [thisr], 'o')
ax.annotate('a polar annotation',
            xy=(thistheta, thisr),  # theta, radius
            xytext=(0.05, 0.05),    # fraction, fraction
            textcoords='figure fraction',
            arrowprops=dict(facecolor='black', shrink=0.05),
            horizontalalignment='left',
            verticalalignment='bottom',
            )
plt.show()

(Source code, png, pdf)

For more on all the wild and wonderful things you can do with annotations, including fancy arrows, see Advanced Annotation and pylab_examples example code: annotation_demo.py.

Do not proceed unless you have already read Basic annotation, text() and annotate()!

Advanced Annotation

Annotating with Text with Box

Let’s start with a simple example.

(Source code, png, pdf)

The text() function in the pyplot module (or text method of the Axes class) takes bbox keyword argument, and when given, a box around the text is drawn.

bbox_props = dict(boxstyle="rarrow,pad=0.3", fc="cyan", ec="b", lw=2)
t = ax.text(0, 0, "Direction", ha="center", va="center", rotation=45,
            size=15,
            bbox=bbox_props)

The patch object associated with the text can be accessed by:

bb = t.get_bbox_patch()

The return value is an instance of FancyBboxPatch and the patch properties like facecolor, edgewidth, etc. can be accessed and modified as usual. To change the shape of the box, use the set_boxstyle method.

bb.set_boxstyle("rarrow", pad=0.6)

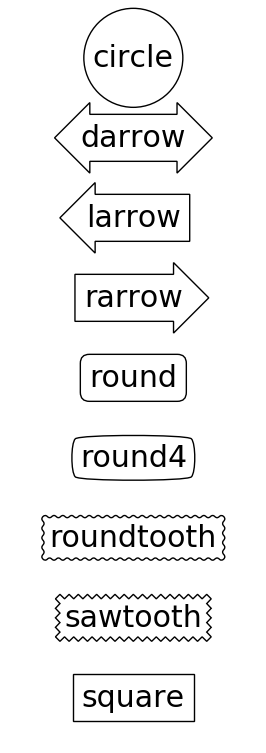
The arguments are the name of the box style with its attributes as keyword arguments. Currently, following box styles are implemented.

Class	Name	Attrs
Circle	circle	pad=0.3
DArrow	darrow	pad=0.3
LArrow	larrow	pad=0.3
RArrow	rarrow	pad=0.3
Round	round	pad=0.3,rounding_size=None
Round4	round4	pad=0.3,rounding_size=None
Roundtooth	roundtooth	pad=0.3,tooth_size=None
Sawtooth	sawtooth	pad=0.3,tooth_size=None
Square	square	pad=0.3

(Source code, png, pdf)

Note that the attribute arguments can be specified within the style name with separating comma (this form can be used as “boxstyle” value of bbox argument when initializing the text instance)

bb.set_boxstyle("rarrow,pad=0.6")

Annotating with Arrow

The annotate() function in the pyplot module (or annotate method of the Axes class) is used to draw an arrow connecting two points on the plot.

ax.annotate("Annotation",
            xy=(x1, y1), xycoords='data',
            xytext=(x2, y2), textcoords='offset points',
            )

This annotates a point at xy in the given coordinate (xycoords) with the text at xytext given in textcoords. Often, the annotated point is specified in the data coordinate and the annotating text in offset points. See annotate() for available coordinate systems.

An arrow connecting two points (xy & xytext) can be optionally drawn by specifying the arrowprops argument. To draw only an arrow, use empty string as the first argument.

ax.annotate("",
            xy=(0.2, 0.2), xycoords='data',
            xytext=(0.8, 0.8), textcoords='data',
            arrowprops=dict(arrowstyle="->",
                            connectionstyle="arc3"),
            )

(Source code, png, pdf)

The arrow drawing takes a few steps.

1. a connecting path between two points are created. This is controlled by connectionstyle key value.
2. If patch object is given (patchA & patchB), the path is clipped to avoid the patch.
3. The path is further shrunk by given amount of pixels (shrinkA & shrinkB)
4. The path is transmuted to arrow patch, which is controlled by the arrowstyle key value.

(Source code, png, pdf)

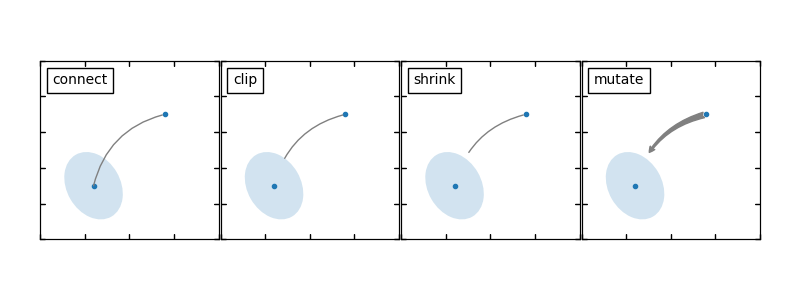
The creation of the connecting path between two points is controlled by connectionstyle key and the following styles are available.

Name	Attrs
angle	angleA=90,angleB=0,rad=0.0
angle3	angleA=90,angleB=0
arc	angleA=0,angleB=0,armA=None,armB=None,rad=0.0
arc3	rad=0.0
bar	armA=0.0,armB=0.0,fraction=0.3,angle=None

Note that “3” in angle3 and arc3 is meant to indicate that the resulting path is a quadratic spline segment (three control points). As will be discussed below, some arrow style options can only be used when the connecting path is a quadratic spline.

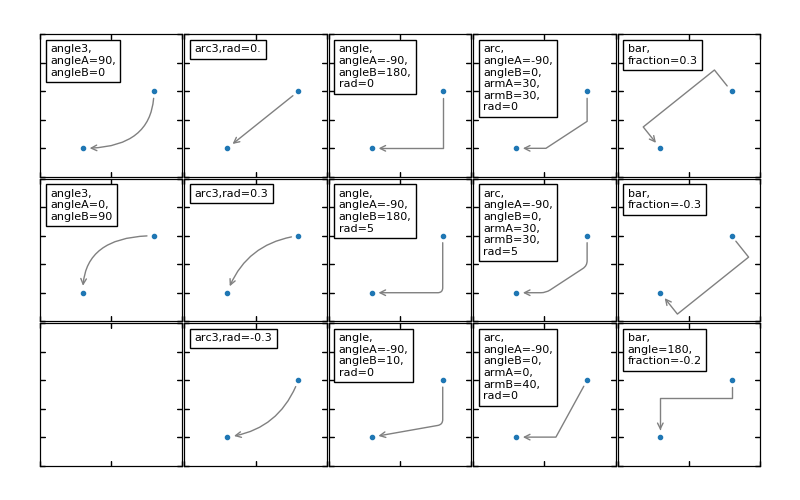
The behavior of each connection style is (limitedly) demonstrated in the example below. (Warning : The behavior of the bar style is currently not well defined, it may be changed in the future).

(Source code, png, pdf)

The connecting path (after clipping and shrinking) is then mutated to an arrow patch, according to the given arrowstyle.

Name	Attrs
-	None
->	head_length=0.4,head_width=0.2
-[	widthB=1.0,lengthB=0.2,angleB=None
|-|	widthA=1.0,widthB=1.0
-|>	head_length=0.4,head_width=0.2
<-	head_length=0.4,head_width=0.2
<->	head_length=0.4,head_width=0.2
<|-	head_length=0.4,head_width=0.2
<|-|>	head_length=0.4,head_width=0.2
fancy	head_length=0.4,head_width=0.4,tail_width=0.4
simple	head_length=0.5,head_width=0.5,tail_width=0.2
wedge	tail_width=0.3,shrink_factor=0.5

(Source code, png, pdf)

Some arrowstyles only work with connection styles that generate a quadratic-spline segment. They are fancy, simple, and wedge. For these arrow styles, you must use the “angle3” or “arc3” connection style.

If the annotation string is given, the patchA is set to the bbox patch of the text by default.

(Source code, png, pdf)

As in the text command, a box around the text can be drawn using the bbox argument.

(Source code, png, pdf)

By default, the starting point is set to the center of the text extent. This can be adjusted with relpos key value. The values are normalized to the extent of the text. For example, (0,0) means lower-left corner and (1,1) means top-right.

(Source code, png, pdf)

Placing Artist at the anchored location of the Axes

There are classes of artists that can be placed at an anchored location in the Axes. A common example is the legend. This type of artist can be created by using the OffsetBox class. A few predefined classes are available in mpl_toolkits.axes_grid.anchored_artists.

from mpl_toolkits.axes_grid.anchored_artists import AnchoredText
at = AnchoredText("Figure 1a",
                  prop=dict(size=8), frameon=True,
                  loc=2,
                  )
at.patch.set_boxstyle("round,pad=0.,rounding_size=0.2")
ax.add_artist(at)

(Source code, png, pdf)

The loc keyword has same meaning as in the legend command.

A simple application is when the size of the artist (or collection of artists) is known in pixel size during the time of creation. For example, If you want to draw a circle with fixed size of 20 pixel x 20 pixel (radius = 10 pixel), you can utilize AnchoredDrawingArea. The instance is created with a size of the drawing area (in pixels), and arbitrary artists can added to the drawing area. Note that the extents of the artists that are added to the drawing area are not related to the placement of the drawing area itself. Only the initial size matters.

from mpl_toolkits.axes_grid.anchored_artists import AnchoredDrawingArea

ada = AnchoredDrawingArea(20, 20, 0, 0,
                          loc=1, pad=0., frameon=False)
p1 = Circle((10, 10), 10)
ada.drawing_area.add_artist(p1)
p2 = Circle((30, 10), 5, fc="r")
ada.drawing_area.add_artist(p2)

The artists that are added to the drawing area should not have a transform set (it will be overridden) and the dimensions of those artists are interpreted as a pixel coordinate, i.e., the radius of the circles in above example are 10 pixels and 5 pixels, respectively.

(Source code, png, pdf)

Sometimes, you want your artists to scale with the data coordinate (or coordinates other than canvas pixels). You can use AnchoredAuxTransformBox class. This is similar to AnchoredDrawingArea except that the extent of the artist is determined during the drawing time respecting the specified transform.

from mpl_toolkits.axes_grid.anchored_artists import AnchoredAuxTransformBox

box = AnchoredAuxTransformBox(ax.transData, loc=2)
el = Ellipse((0,0), width=0.1, height=0.4, angle=30)  # in data coordinates!
box.drawing_area.add_artist(el)

The ellipse in the above example will have width and height corresponding to 0.1 and 0.4 in data coordinateing and will be automatically scaled when the view limits of the axes change.

(Source code, png, pdf)

As in the legend, the bbox_to_anchor argument can be set. Using the HPacker and VPacker, you can have an arrangement(?) of artist as in the legend (as a matter of fact, this is how the legend is created).

(Source code, png, pdf)

Note that unlike the legend, the bbox_transform is set to IdentityTransform by default.

Using Complex Coordinates with Annotations

The Annotation in matplotlib supports several types of coordinates as described in Basic annotation. For an advanced user who wants more control, it supports a few other options.

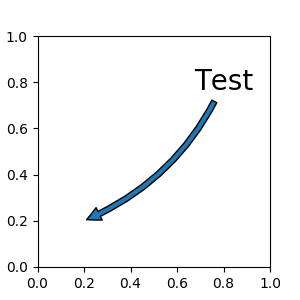
1. Transform instance. For example,

   ax.annotate("Test", xy=(0.5, 0.5), xycoords=ax.transAxes)
   

   is identical to

   ax.annotate("Test", xy=(0.5, 0.5), xycoords="axes fraction")
   

   With this, you can annotate a point in other axes.

   ax1, ax2 = subplot(121), subplot(122)
   ax2.annotate("Test", xy=(0.5, 0.5), xycoords=ax1.transData,
                xytext=(0.5, 0.5), textcoords=ax2.transData,
                arrowprops=dict(arrowstyle="->"))
   

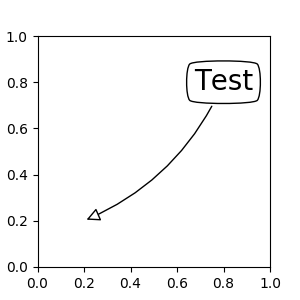
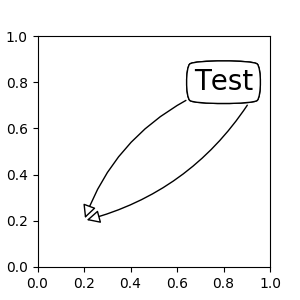
2. Artist instance. The xy value (or xytext) is interpreted as a fractional coordinate of the bbox (return value of get_window_extent) of the artist.

   an1 = ax.annotate("Test 1", xy=(0.5, 0.5), xycoords="data",
                     va="center", ha="center",
                     bbox=dict(boxstyle="round", fc="w"))
   an2 = ax.annotate("Test 2", xy=(1, 0.5), xycoords=an1, # (1,0.5) of the an1's bbox
                     xytext=(30,0), textcoords="offset points",
                     va="center", ha="left",
                     bbox=dict(boxstyle="round", fc="w"),
                     arrowprops=dict(arrowstyle="->"))
   

   (Source code, png, pdf)

   

   Note that it is your responsibility that the extent of the coordinate artist (an1 in above example) is determined before an2 gets drawn. In most cases, it means that an2 needs to be drawn later than an1.

3. A callable object that returns an instance of either BboxBase or Transform. If a transform is returned, it is the same as 1 and if a bbox is returned, it is the same as 2. The callable object should take a single argument of the renderer instance. For example, the following two commands give identical results

   an2 = ax.annotate("Test 2", xy=(1, 0.5), xycoords=an1,
                     xytext=(30,0), textcoords="offset points")
   an2 = ax.annotate("Test 2", xy=(1, 0.5), xycoords=an1.get_window_extent,
                     xytext=(30,0), textcoords="offset points")
   

4. A tuple of two coordinate specifications. The first item is for the x-coordinate and the second is for the y-coordinate. For example,

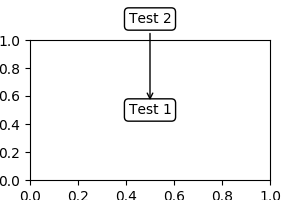
   annotate("Test", xy=(0.5, 1), xycoords=("data", "axes fraction"))
   

   0.5 is in data coordinates, and 1 is in normalized axes coordinates. You may use an artist or transform as with a tuple. For example,

   import matplotlib.pyplot as plt
   
   plt.figure(figsize=(3,2))
   ax=plt.axes([0.1, 0.1, 0.8, 0.7])
   an1 = ax.annotate("Test 1", xy=(0.5, 0.5), xycoords="data",
                     va="center", ha="center",
                     bbox=dict(boxstyle="round", fc="w"))
   
   an2 = ax.annotate("Test 2", xy=(0.5, 1.), xycoords=an1,
                     xytext=(0.5,1.1), textcoords=(an1, "axes fraction"),
                     va="bottom", ha="center",
                     bbox=dict(boxstyle="round", fc="w"),
                     arrowprops=dict(arrowstyle="->"))
   plt.show()
   

   (Source code, png, pdf)

   

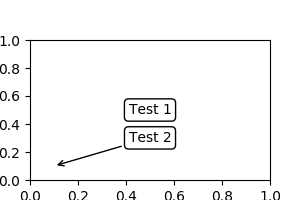
5. Sometimes, you want your annotation with some “offset points”, not from the annotated point but from some other point. OffsetFrom is a helper class for such cases.

   import matplotlib.pyplot as plt
   
   plt.figure(figsize=(3,2))
   ax=plt.axes([0.1, 0.1, 0.8, 0.7])
   an1 = ax.annotate("Test 1", xy=(0.5, 0.5), xycoords="data",
                     va="center", ha="center",
                     bbox=dict(boxstyle="round", fc="w"))
   
   from matplotlib.text import OffsetFrom
   offset_from = OffsetFrom(an1, (0.5, 0))
   an2 = ax.annotate("Test 2", xy=(0.1, 0.1), xycoords="data",
                     xytext=(0, -10), textcoords=offset_from,
                     # xytext is offset points from "xy=(0.5, 0), xycoords=an1"
                     va="top", ha="center",
                     bbox=dict(boxstyle="round", fc="w"),
                     arrowprops=dict(arrowstyle="->"))
   plt.show()
   

   (Source code, png, pdf)

   

   You may take a look at this example pylab_examples example code: annotation_demo3.py.

Using ConnectorPatch

The ConnectorPatch is like an annotation without text. While the annotate function is recommended in most situations, the ConnectorPatch is useful when you want to connect points in different axes.

from matplotlib.patches import ConnectionPatch
xy = (0.2, 0.2)
con = ConnectionPatch(xyA=xy, xyB=xy, coordsA="data", coordsB="data",
                      axesA=ax1, axesB=ax2)
ax2.add_artist(con)

The above code connects point xy in the data coordinates of ax1 to point xy in the data coordinates of ax2. Here is a simple example.

(Source code, png, pdf)

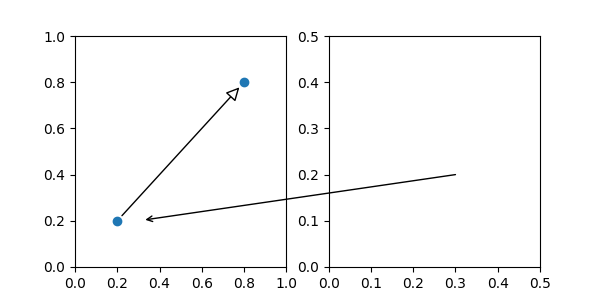
While the ConnectorPatch instance can be added to any axes, you may want to add it to the axes that is latest in drawing order to prevent overlap by other axes.

Advanced Topics

Zoom effect between Axes

mpl_toolkits.axes_grid.inset_locator defines some patch classes useful for interconnecting two axes. Understanding the code requires some knowledge of how mpl’s transform works. But, utilizing it will be straight forward.

(Source code, png, pdf)

Define Custom BoxStyle

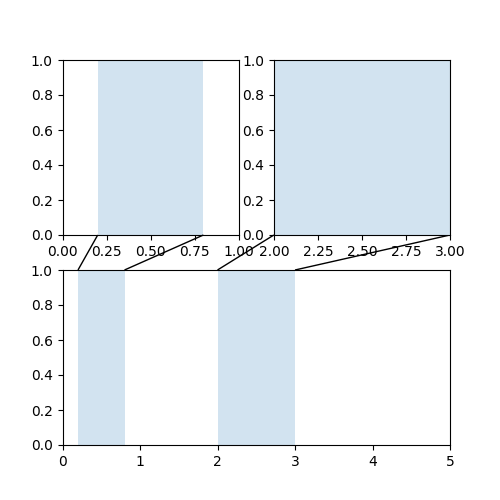
You can use a custom box style. The value for the boxstyle can be a callable object in the following forms.:

def __call__(self, x0, y0, width, height, mutation_size,
             aspect_ratio=1.):
    """
    Given the location and size of the box, return the path of
    the box around it.

      - *x0*, *y0*, *width*, *height* : location and size of the box
      - *mutation_size* : a reference scale for the mutation.
      - *aspect_ratio* : aspect-ratio for the mutation.
    """
    path = ...
    return path

Here is a complete example.

(Source code, png, pdf)

However, it is recommended that you derive from the matplotlib.patches.BoxStyle._Base as demonstrated below.

from matplotlib.path import Path
from matplotlib.patches import BoxStyle
import matplotlib.pyplot as plt

# we may derive from matplotlib.patches.BoxStyle._Base class.
# You need to override transmute method in this case.

class MyStyle(BoxStyle._Base):
    """
    A simple box.
    """

    def __init__(self, pad=0.3):
        """
        The arguments need to be floating numbers and need to have
        default values.

         *pad*
            amount of padding
        """

        self.pad = pad
        super(MyStyle, self).__init__()

    def transmute(self, x0, y0, width, height, mutation_size):
        """
        Given the location and size of the box, return the path of
        the box around it.

         - *x0*, *y0*, *width*, *height* : location and size of the box
         - *mutation_size* : a reference scale for the mutation.

        Often, the *mutation_size* is the font size of the text.
        You don't need to worry about the rotation as it is
        automatically taken care of.
        """

        # padding
        pad = mutation_size * self.pad

        # width and height with padding added.
        width, height = width + 2.*pad, \
                        height + 2.*pad,

        # boundary of the padded box
        x0, y0 = x0-pad, y0-pad,
        x1, y1 = x0+width, y0 + height

        cp = [(x0, y0),
              (x1, y0), (x1, y1), (x0, y1),
              (x0-pad, (y0+y1)/2.), (x0, y0),
              (x0, y0)]

        com = [Path.MOVETO,
               Path.LINETO, Path.LINETO, Path.LINETO,
               Path.LINETO, Path.LINETO,
               Path.CLOSEPOLY]

        path = Path(cp, com)

        return path


# register the custom style
BoxStyle._style_list["angled"] = MyStyle

plt.figure(1, figsize=(3,3))
ax = plt.subplot(111)
ax.text(0.5, 0.5, "Test", size=30, va="center", ha="center", rotation=30,
        bbox=dict(boxstyle="angled,pad=0.5", alpha=0.2))

del BoxStyle._style_list["angled"]

plt.show()

(Source code, png, pdf)

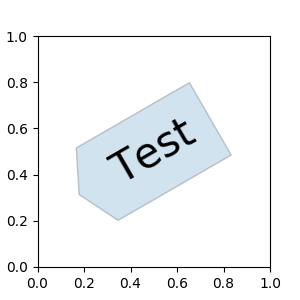
Similarly, you can define a custom ConnectionStyle and a custom ArrowStyle. See the source code of lib/matplotlib/patches.py and check how each style class is defined.