| Oracle® Spatial Developer's Guide 11g Release 2 (11.2) Part Number E11830-11 |
|
|
PDF · Mobi · ePub |
| Oracle® Spatial Developer's Guide 11g Release 2 (11.2) Part Number E11830-11 |
|
|
PDF · Mobi · ePub |
Linear referencing is a natural and convenient means to associate attributes or events to locations or portions of a linear feature. It has been widely used in transportation applications (such as for highways, railroads, and transit routes) and utilities applications (such as for gas and oil pipelines). The major advantage of linear referencing is its capability of locating attributes and events along a linear feature with only one parameter (usually known as measure) instead of two (such as longitude/latitude or x/y in Cartesian space). Sections of a linear feature can be referenced and created dynamically by indicating the start and end locations along the feature without explicitly storing them.
The linear referencing system (LRS) application programming interface (API) in Oracle Spatial provides server-side LRS capabilities at the cartographic level. The linear measure information is directly integrated into the Oracle Spatial geometry structure. The Oracle Spatial LRS API provides support for dynamic segmentation, and it serves as a groundwork for third-party or middle-tier application development for virtually any linear referencing methods and models in any coordinate system.
For an example of LRS, see Section 7.7. However, you may want to read the rest of this chapter first, to understand the concepts that the example illustrates.
For reference information about LRS functions and procedures, see Chapter 25.
This chapter contains the following major sections:
This section explains important terms and concepts related to linear referencing support in Oracle Spatial.
Geometric segments are basic LRS elements in Oracle Spatial. A geometric segment can be any of the following:
Line string: an ordered, nonbranching, and continuous geometry (for example, a simple road)
Multiline string: nonconnected line strings (for example, a highway with a gap caused by a lake or a bypass road)
Polygon (for example, a racetrack or a scenic tour route that starts and ends at the same point)
A geometric segment must contain at least start and end measures for its start and end points. Measures of points of interest (such as highway exits) on the geometric segments can also be assigned. These measures are either assigned by users or derived from existing geometric segments. Figure 7-1 shows a geometric segment with four line segments and one arc. Points on the geometric segment are represented by triplets (x, y, m), where x and y describe the location and m denotes the measure (with each measure value underlined in Figure 7-1).
Shape points are points that are specified when an LRS segment is constructed, and that are assigned measure information. In Oracle Spatial, a line segment is represented by its start and end points, and an arc is represented by three points: start, middle, and end points of the arc. You must specify these points as shape points, but you can also specify other points as shape points if you need measure information stored for these points (for example, an exit in the middle of a straight part of the highway).
Thus, shape points can serve one or both of the following purposes: to indicate the direction of the segment (for example, a turn or curve), and to identify a point of interest for which measure information is to be stored.
Shape points might not directly relate to mileposts or reference posts in LRS; they are used as internal reference points. The measure information of shape points is automatically populated when you define the LRS segment using the SDO_LRS.DEFINE_GEOM_SEGMENT procedure, which is described in Chapter 25.
The direction of a geometric segment is indicated from the start point of the geometric segment to the end point. The direction is determined by the order of the vertices (from start point to end point) in the geometry definition. Measures of points on a geometric segment always either increase or decrease along the direction of the geometric segment.
The measure of a point along a geometric segment is the linear distance (in the measure dimension) to the point measured from the start point (for increasing values) or end point (for decreasing values) of the geometric segment. The measure information does not necessarily have to be of the same scale as the distance. However, the linear mapping relationship between measure and distance is always preserved.
Some LRS functions use offset instead of measure to represent measured distance along linear features. Although some other linear referencing systems might use offset to mean what the Oracle Spatial LRS refers to as measure, offset has a different meaning in Oracle Spatial from measure, as explained in Section 7.1.5.
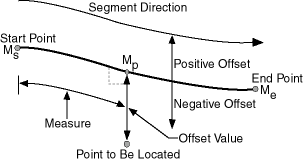
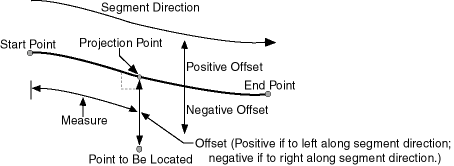
The offset of a point along a geometric segment is the perpendicular distance between the point and the geometric segment. Offsets are positive if the points are on the left side along the segment direction and are negative if they are on the right side. Points are on a geometric segment if their offsets to the segment are zero.
The unit of measurement for an offset is the same as for the coordinate system associated with the geometric segment. For geodetic data, the default unit of measurement is meters.
Figure 7-2 shows how a point can be located along a geometric segment with measure and offset information. By assigning an offset together with a measure, it is possible to locate not only points that are on the geometric segment, but also points that are perpendicular to the geometric segment.
Figure 7-2 Describing a Point Along a Segment with a Measure and an Offset
Any unassigned measures of a geometric segment are automatically populated based upon their distance distribution. This is done before any LRS operations for geometric segments with unknown measures (NULL in Oracle Spatial). The resulting geometric segments from any LRS operations return the measure information associated with geometric segments. The measure of a point on the geometric segment can be obtained based upon a linear mapping relationship between its previous and next known measures or locations. See the algorithm representation in Figure 7-3 and the example in Figure 7-4.
Figure 7-3 Measures, Distances, and Their Mapping Relationship
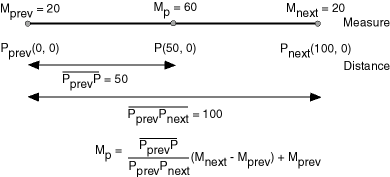
Figure 7-4 Measure Populating of a Geometric Segment
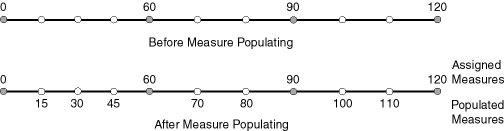
Measures are evenly spaced between assigned measures. However, the assigned measures for points of interest on a geometric segment do not need to be evenly spaced. This could eliminate the problem of error accumulation and account for inaccuracy of data source.
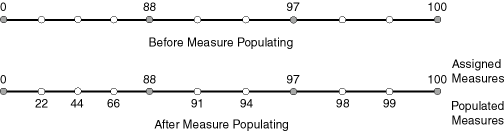
Moreover, the assigned measures do not even need to reflect actual distances (for example, they can reflect estimated driving time); they can be any valid values within the measure range. Figure 7-5 shows the measure population that results when assigned measure values are not proportional and reflect widely varying gaps.
Figure 7-5 Measure Populating with Disproportional Assigned Measures
In all cases, measure populating is done in an incremental fashion along the segment direction. This improves the performance of current and subsequent LRS operations.
The start and end measures of a geometric segment define the linear measure range of the geometric segment. Any valid LRS measures of a geometric segment must fall within its linear measure range.
The projection of a point along a geometric segment is the point on the geometric segment with the minimum distance to the specified point. The measure information of the resulting point is also returned in the point geometry.
LRS points are points with linear measure information along a geometric segment. A valid LRS point is a point geometry with measure information.
All LRS point data must be stored in the SDO_ELEM_INFO_ARRAY and SDO_ORDINATE_ARRAY, and cannot be stored in the SDO_POINT field in the SDO_GEOMETRY definition of the point.
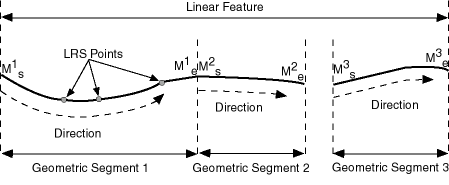
Linear features are any spatial objects that can be treated as a logical set of linear segments. Examples of linear features are highways in transportation applications and pipelines in utility industry applications. The relationship of linear features, geometric segments, and LRS points is shown in Figure 7-6, where a single linear feature consists of three geometric segments, and three LRS points are shown on the first segment.
Figure 7-6 Linear Feature, Geometric Segments, and LRS Points
With a multiline string or polygon with hole LRS geometry, the SDO_LRS.DEFINE_GEOM_SEGMENT procedure and SDO_LRS.CONVERT_TO_LRS_GEOM function by default assign the same measure value to the end point of one segment and the start point (separated by a gap) of the next segment, although you can later assign different measure values to points. Thus, by default there will duplicate measure values in different segments for such geometries. In such cases, LRS subprograms use the first point with a specified measure, except when doing so would result in an invalid geometry.
For example, assume that in a multiline string LRS geometry, the first segment is from measures 0 through 100 and the second segment is from measures 100 through 150. If you use the SDO_LRS.LOCATE_PT function to find the point at measure 100, the returned point will be at measure 100 in the first segment. If you use the SDO_LRS.CLIP_GEOM_SEGMENT, SDO_LRS.DYNAMIC_SEGMENT, or SDO_LRS.OFFSET_GEOM_SEGMENT function to return the geometry object between measures 75 and 125, the result is a multiline string geometry consisting of two segments. If you use the same function to return the geometry object between measures 100 and 125, the point at measure 100 in the first segment is ignored, and the result is a line string along the second segment from measures 100 through 125.
The Oracle Spatial LRS data model incorporates measure information into its geometry representation at the point level. The measure information is directly integrated into the Oracle Spatial model. To accomplish this, an additional measure dimension must be added to the Oracle Spatial metadata.
Oracle Spatial LRS support affects the Spatial metadata and data (the geometries). Example 7-1 shows how a measure dimension can be added to two-dimensional geometries in the Spatial metadata. The measure dimension must be the last element of the SDO_DIM_ARRAY in a spatial object definition (shown in bold in Example 7-1).
Example 7-1 Including LRS Measure Dimension in Spatial Metadata
INSERT INTO user_sdo_geom_metadata
(TABLE_NAME,
COLUMN_NAME,
DIMINFO,
SRID)
VALUES(
'LRS_ROUTES',
'GEOMETRY',
SDO_DIM_ARRAY (
SDO_DIM_ELEMENT('X', 0, 20, 0.005),
SDO_DIM_ELEMENT('Y', 0, 20, 0.005),
SDO_DIM_ELEMENT('M', 0, 100, 0.005)),
NULL);
After adding the new measure dimension, geometries with measure information such as geometric segments and LRS points can be represented. An example of creating a geometric segment with three line segments is shown in Figure 7-7.
In Figure 7-7, the geometric segment has the following definition (with measure values underlined):
SDO_GEOMETRY(3302, NULL, NULL,
SDO_ELEM_INFO_ARRAY(1,2,1),
SDO_ORDINATE_ARRAY(5,10,0, 20,5,NULL, 35,10,NULL, 55,10,100))
Whenever a geometric segment is defined, its start and end measures must be defined or derived from some existing geometric segment. The unsigned measures of all shape points on a geometric segment will be automatically populated.
The SDO_GTYPE of any point geometry used with an LRS function must be 3301.
If LRS data has four dimensions (three plus the M dimension) and if you need to index all three non-measure dimensions, you must use a spatial R-tree index to index the data, and you must specify PARAMETERS('sdo_indx_dims=3') in the CREATE INDEX statement to ensure that the first three dimensions are indexed. Note, however, that if you specify an sdo_indx_dims value of 3 or higher, only those operators listed in Section 1.11 as considering all three dimensions can be used on the indexed geometries; the other operators described in Chapter 19 cannot be used. (The default value for the sdo_indx_dims keyword is 2, which would cause only the first two dimensions to be indexed.) For example, if the dimensions are X, Y, Z, and M, specify sdo_indx_dims=3 to index the X, Y, and Z dimensions, but not the measure (M) dimension. Do not include the measure dimension in a spatial index, because this causes additional processing overhead and produces no benefit.
Information about the CREATE INDEX statement and its parameters and keywords is in Chapter 18.
Most LRS functions have formats that end in _3D: for example, DEFINE_GEOM_SEGMENT_3D, CLIP_GEOM_SEGMENT_3D, FIND_MEASURE_3D, and LOCATE_PT_3D. If a function has a 3D format, it is identified in the Usage Notes for the function in Chapter 25.
The 3D formats are supported only for line string and multiline string geometries. The 3D formats should be used only when the geometry object has four dimensions and the fourth dimension is the measure (for example, X, Y, Z, and M), and only when you want the function to consider the first three dimensions (for example, X, Y, and Z). If the standard format of a function (that is, without the _3D) is used on a geometry with four dimensions, the function considers only the first two dimensions (for example, X and Y).
For example, the following format considers the X, Y, and Z dimensions of the specified GEOM object in performing the clip operation:
SELECT SDO_LRS.CLIP_GEOM_SEGMENT_3D(a.geom, m.diminfo, 5, 10)
FROM routes r, user_sdo_geom_metadata m
WHERE m.table_name = 'ROUTES' AND m.column_name = 'GEOM'
AND r.route_id = 1;
However, the following format considers only the X and Y dimensions, and ignores the Z dimension, of the specified GEOM object in performing the clip operation:
SELECT SDO_LRS.CLIP_GEOM_SEGMENT(a.geom, m.diminfo, 5, 10)
FROM routes r, user_sdo_geom_metadata m
WHERE m.table_name = 'ROUTES' AND m.column_name = 'GEOM'
AND r.route_id = 1;
The parameters for the standard and 3D formats of any function are the same, and the Usage Notes apply to both formats.
The 3D formats are not supported with the following:
Geodetic data
Polygons, arcs, or circles
This section describes several linear referencing operations supported by the Oracle Spatial LRS API.
There are two ways to create a geometric segment with measure information:
Construct a geometric segment and assign measures explicitly.
Define a geometric segment with specified start and end, and any other measures, in an ascending or descending order. Measures of shape points with unknown (unassigned) measures (null values) in the geometric segment will be automatically populated according to their locations and distance distribution.
Figure 7-8 shows different ways of defining a geometric segment:
An LRS segment must be defined (or must already exist) before any LRS operations can proceed. That is, the start, end, and any other assigned measures must be present to derive the location from a specified measure. The measure information of intermediate shape points will automatically be populated if measure values are not assigned.
You can redefine a geometric segment to replace the existing measures of all shape points between the start and end point with automatically calculated measures. Redefining a segment can be useful if errors have been made in one or more explicit measure assignments, and you want to start over with proportionally assigned measures.
Figure 7-9 shows the redefinition of a segment where the existing (before) assigned measure values are not proportional and reflect widely varying gaps.
Figure 7-9 Redefining a Geometric Segment
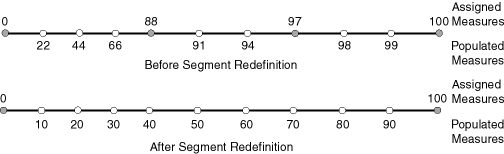
After the segment redefinition in Figure 7-9, the populated measures reflect proportional distances along the segment.
You can clip a geometric segment to create a new geometric segment out of an existing geometric segment, as shown in Figure 7-10, part a.
Figure 7-10 Clipping, Splitting, and Concatenating Geometric Segments
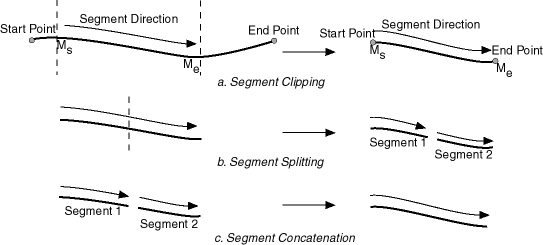
In Figure 7-10, part a, a segment is created from part of a larger segment. The new segment has its own start and end points, and the direction is the same as in the original larger segment.
You can create two new geometric segments by splitting a geometric segment, as shown in Figure 7-10, part b. The direction of each new segment is the same as in the original segment.
Note:
In Figure 7-10 and several figures that follow, small gaps between segments are used in illustrations of segment splitting and concatenation. Each gap simply reinforces the fact that two different segments are involved. However, the two segments (such as segment 1 and segment 2 in Figure 7-10, parts b and c) are actually connected. The tolerance (see Section 1.5.5) is considered in determining whether or not segments are connected.You can create a new geometric segment by concatenating two geometric segments, as shown in Figure 7-10, part c. The geometric segments do not need to be spatially connected, although they are connected in the illustration in Figure 7-10, part c. (If the segments are not spatially connected, the concatenated result is a multiline string.) The measures of the second geometric segment are shifted so that the end measure of the first segment is the same as the start measure of the second segment. The direction of the segment resulting from the concatenation is the same as in the two original segments.
Measure assignments for the clipping, splitting, and concatenating operations in Figure 7-10 are shown in Figure 7-11. Measure information and segment direction are preserved in a consistent manner. The assignment is done automatically when the operations have completed.
Figure 7-11 Measure Assignment in Geometric Segment Operations
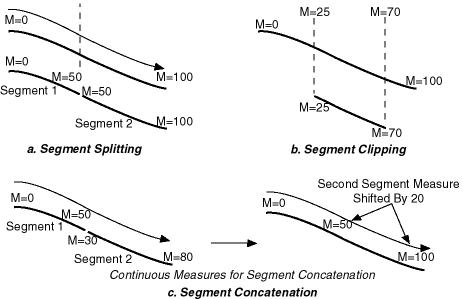
The direction of the geometric segment resulting from concatenation is always the direction of the first segment (geom_segment1 in the call to the SDO_LRS.CONCATENATE_GEOM_SEGMENTS function), as shown in Figure 7-12.
Figure 7-12 Segment Direction with Concatenation
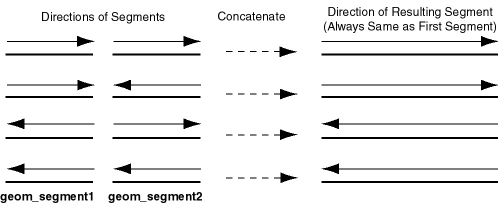
In addition to explicitly concatenating two connected segments using the SDO_LRS.CONCATENATE_GEOM_SEGMENTS function, you can perform aggregate concatenation: that is, you can concatenate all connected geometric segments in a column (layer) using the SDO_AGGR_LRS_CONCAT spatial aggregate function. (See the description and example of the SDO_AGGR_LRS_CONCAT spatial aggregate function in Chapter 20.)
You can create a new geometric segment by performing a linear scaling operation on a geometric segment. Figure 7-13 shows the mapping relationship for geometric segment scaling.
In general, scaling a geometric segment only involves rearranging measures of the newly created geometric segment. However, if the scaling factor is negative, the order of the shape points needs to be reversed so that measures will increase along the geometric segment's direction (which is defined by the order of the shape points).
A scale operation can perform any combination of the following operations:
Translating (shifting) measure information. (For example, add the same value to Ms and Me to get M's and M'e.)
Reversing measure information. (Let M's = Me, M'e = Ms, and Mshift = 0.)
Performing simple scaling of measure information. (Let Mshift = 0.)
For examples of these operations, see the Usage Notes and Examples for theSDO_LRS.SCALE_GEOM_SEGMENT, SDO_LRS.TRANSLATE_MEASURE, SDO_LRS.REVERSE_GEOMETRY, and SDO_LRS.REDEFINE_GEOM_SEGMENT subprograms in Chapter 25.
You can create a new geometric segment by performing an offsetting operation on a geometric segment. Figure 7-14 shows the mapping relationship for geometric segment offsetting.
Figure 7-14 Offsetting a Geometric Segment

In the offsetting operation shown in Figure 7-14, the resulting geometric segment is offset by 5 units from the specified start and end measures of the original segment.
For more information, see the Usage Notes and Examples for the SDO_LRS.OFFSET_GEOM_SEGMENT function in Chapter 25.
You can find the position of a point described by a measure and an offset on a geometric segment (see Figure 7-15).
Figure 7-15 Locating a Point Along a Segment with a Measure and an Offset
There is always a unique location with a specific measure on a geometric segment. Ambiguity arises when offsets are given and the points described by the measures fall on shape points of the geometric segment (see Figure 7-16).
Figure 7-16 Ambiguity in Location Referencing with Offsets
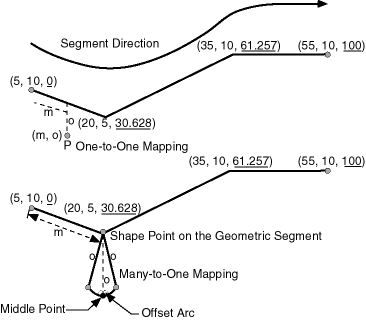
As shown in Figure 7-16, an offset arc of a shape point on a geometric segment is an arc on which all points have the same minimum distance to the shape point. As a result, all points on the offset arc are represented by the same (measure, offset) pair. To resolve this one-to-many mapping problem, the middle point on the offset arc is returned.
You can find the projection point of a point with respect to a geometric segment. The point to be projected can be on or off the segment. If the point is on the segment, the point and its projection point are the same.
Projection is a reverse operation of the point-locating operation shown in Figure 7-15. Similar to a point-locating operation, all points on the offset arc of a shape point will have the same projection point (that is, the shape point itself), measure, and offset (see Figure 7-16). If there are multiple projection points for a point, the first one from the start point is returned (Projection Point 1 in both illustrations in Figure 7-17).
You can convert geometries from standard line string format to LRS format, and the reverse. The main use of conversion functions will probably occur if you have a large amount of existing line string data, in which case conversion is a convenient alternative to creating all of the LRS segments manually. However, if you need to convert LRS segments to standard line strings for certain applications, that capability is provided also.
Functions are provided to convert:
Individual line strings or points
For conversion from standard format to LRS format, a measure dimension (named M by default) is added, and measure information is provided for each point. For conversion from LRS format to standard format, the measure dimension and information are removed. In both cases, the dimensional information (DIMINFO) metadata in the USER_SDO_GEOM_METADATA view is not affected.
Layers (all geometries in a column)
For conversion from standard format to LRS format, a measure dimension (named M by default) is added, but no measure information is provided for each point. For conversion from LRS format to standard format, the measure dimension and information are removed. In both cases, the dimensional information (DIMINFO) metadata in the USER_SDO_GEOM_METADATA view is modified as needed.
Dimensional information (DIMINFO)
The dimensional information (DIMINFO) metadata in the USER_SDO_GEOM_METADATA view is modified as needed. For example, converting a standard dimensional array with X and Y dimensions (SDO_DIM_ELEMENT) to an LRS dimensional array causes an M dimension (SDO_DIM_ELEMENT) to be added.
Figure 7-18 shows the addition of measure information when a standard line string is converted to an LRS line string (using the SDO_LRS.CONVERT_TO_LRS_GEOM function). The measure dimension values are underlined in Figure 7-18.
Figure 7-18 Conversion from Standard to LRS Line String
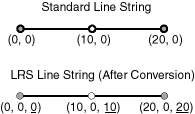
For conversions of point geometries, the SDO_POINT attribute (described in Section 2.2.3) in the returned geometry is affected as follows:
If a standard point is converted to an LRS point, the SDO_POINT attribute information in the input geometry is used to set the SDO_ELEM_INFO and SDO_ORDINATES attributes (described in Section 2.2.4 and Section 2.2.5) in the resulting geometry, and the SDO_POINT attribute in the resulting geometry is set to null.
If an LRS point is converted to a standard point, the information in the SDO_ELEM_INFO and SDO_ORDINATES attributes (described in Section 2.2.4 and Section 2.2.5) in the input geometry is used to set the SDO_POINT attribute information in the resulting geometry, and the SDO_ELEM_INFO and SDO_ORDINATES attributes in the resulting geometry are set to null.
The conversion functions are listed in Table 25-3 in Chapter 25. See also the reference information in Chapter 25 about each conversion function.
Many LRS functions require that you specify a tolerance value or one or more dimensional arrays. Thus, you can control whether to specify a single tolerance value for all non-measure dimensions or to use the tolerance associated with each non-measure dimension in the dimensional array or arrays. The tolerance is applied only to the geometry portion of the data, not to the measure dimension. The tolerance value for geodetic data is in meters, and for non-geodetic data it is in the unit of measurement associated with the data. (For a detailed discussion of tolerance, see Section 1.5.5.)
Be sure that the tolerance value used is appropriate to the data and your purpose. If the results of LRS functions seem imprecise or incorrect, you may need to specify a smaller tolerance value.
For clip operations (see Section 7.5.3) and offset operations (see Section 7.5.7), if the returned segment has any shape points within the tolerance value of the input geometric segment from what would otherwise be the start point or end point of the returned segment, the shape point is used as the start point or end point of the returned segment. This is done to ensure that the resulting geometry does not contain any redundant vertices, which would cause the geometry to be invalid. For example, assume that the tolerance associated with the geometric segment (non-geodetic data) in Figure 7-19 is 0.5.
Figure 7-19 Segment for Clip Operation Affected by Tolerance
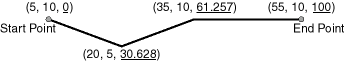
If you request a clip operation to return the segment between measure values 0 (the start point) and 61.5 in Figure 7-19, and if the distance between the points associated with measure values 61.5 and 61.257 is less than the 0.5 tolerance value, the end point of the returned segment is (35, 10, 61.257).
This section presents a simplified example that uses LRS functions. It refers to concepts that are explained in this chapter and uses functions documented in Chapter 25.
This example uses the road that is illustrated in Figure 7-20.
Figure 7-20 Simplified LRS Example: Highway
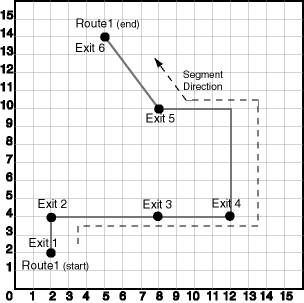
In Figure 7-20, the highway (Route 1) starts at point 2,2 and ends at point 5,14, follows the path shown, and has six entrance-exit points (Exit 1 through Exit 6). For simplicity, each unit on the graph represents one unit of measure, and thus the measure from start to end is 27 (the segment from Exit 5 to Exit 6 being the hypotenuse of a 3-4-5 right triangle).
Each row in Table 7-1 lists an actual highway-related feature and the LRS feature that corresponds to it or that can be used to represent it.
Table 7-1 Highway Features and LRS Counterparts
| Highway Feature | LRS Feature |
|---|---|
|
Named route, road, or street |
LRS segment, or linear feature (logical set of segments) |
|
Mile or kilometer marker |
Measure |
|
Accident reporting and location tracking |
SDO_LRS.LOCATE_PT function |
|
Construction zone (portion of a road) |
SDO_LRS.CLIP_GEOM_SEGMENT function |
|
Road extension (adding at the beginning or end) or combination (designating or renaming two roads that meet as one road) |
SDO_LRS.CONCATENATE_GEOM_SEGMENTS function |
|
Road reconstruction or splitting (resulting in two named roads from one named road) |
SDO_LRS.SPLIT_GEOM_SEGMENT procedure |
|
Finding the closest point on the road to a point off the road (such as a building) |
SDO_LRS.PROJECT_PT function |
|
Guard rail or fence alongside a road |
SDO_LRS.OFFSET_GEOM_SEGMENT function |
Example 7-2 does the following:
Creates a table to hold the segment depicted in Figure 7-20
Inserts the definition of the highway depicted in Figure 7-20 into the table
Inserts the necessary metadata into the USER_SDO_GEOM_METADATA view
Uses PL/SQL and SQL statements to define the segment and perform operations on it
Example 7-3 includes the output of the SELECT statements in Example 7-2.
Example 7-2 Simplified Example: Highway
-- Create a table for routes (highways).
CREATE TABLE lrs_routes (
route_id NUMBER PRIMARY KEY,
route_name VARCHAR2(32),
route_geometry SDO_GEOMETRY);
-- Populate table with just one route for this example.
INSERT INTO lrs_routes VALUES(
1,
'Route1',
SDO_GEOMETRY(
3302, -- line string, 3 dimensions: X,Y,M
NULL,
NULL,
SDO_ELEM_INFO_ARRAY(1,2,1), -- one line string, straight segments
SDO_ORDINATE_ARRAY(
2,2,0, -- Start point - Exit1; 0 is measure from start.
2,4,2, -- Exit2; 2 is measure from start.
8,4,8, -- Exit3; 8 is measure from start.
12,4,12, -- Exit4; 12 is measure from start.
12,10,NULL, -- Not an exit; measure automatically calculated and filled.
8,10,22, -- Exit5; 22 is measure from start.
5,14,27) -- End point (Exit6); 27 is measure from start.
)
);
-- Update the Spatial metadata.
INSERT INTO user_sdo_geom_metadata
(TABLE_NAME,
COLUMN_NAME,
DIMINFO,
SRID)
VALUES (
'lrs_routes',
'route_geometry',
SDO_DIM_ARRAY( -- 20X20 grid
SDO_DIM_ELEMENT('X', 0, 20, 0.005),
SDO_DIM_ELEMENT('Y', 0, 20, 0.005),
SDO_DIM_ELEMENT('M', 0, 20, 0.005) -- Measure dimension
),
NULL -- SRID
);
-- Create the spatial index.
CREATE INDEX lrs_routes_idx ON lrs_routes(route_geometry)
INDEXTYPE IS MDSYS.SPATIAL_INDEX;
-- Test the LRS procedures.
DECLARE
geom_segment SDO_GEOMETRY;
line_string SDO_GEOMETRY;
dim_array SDO_DIM_ARRAY;
result_geom_1 SDO_GEOMETRY;
result_geom_2 SDO_GEOMETRY;
result_geom_3 SDO_GEOMETRY;
BEGIN
SELECT a.route_geometry into geom_segment FROM lrs_routes a
WHERE a.route_name = 'Route1';
SELECT m.diminfo into dim_array from
user_sdo_geom_metadata m
WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY';
-- Define the LRS segment for Route1. This will populate any null measures.
-- No need to specify start and end measures, because they are already defined
-- in the geometry.
SDO_LRS.DEFINE_GEOM_SEGMENT (geom_segment, dim_array);
SELECT a.route_geometry INTO line_string FROM lrs_routes a
WHERE a.route_name = 'Route1';
-- Split Route1 into two segments.
SDO_LRS.SPLIT_GEOM_SEGMENT(line_string,dim_array,5,result_geom_1,result_geom_2);
-- Concatenate the segments that were just split.
result_geom_3 := SDO_LRS.CONCATENATE_GEOM_SEGMENTS(result_geom_1, dim_array, result_geom_2, dim_array);
-- Update and insert geometries into table, to display later.
UPDATE lrs_routes a SET a.route_geometry = geom_segment
WHERE a.route_id = 1;
INSERT INTO lrs_routes VALUES(
11,
'result_geom_1',
result_geom_1
);
INSERT INTO lrs_routes VALUES(
12,
'result_geom_2',
result_geom_2
);
INSERT INTO lrs_routes VALUES(
13,
'result_geom_3',
result_geom_3
);
END;
/
-- First, display the data in the LRS table.
SELECT route_id, route_name, route_geometry FROM lrs_routes;
-- Are result_geom_1 and result_geom2 connected?
SELECT SDO_LRS.CONNECTED_GEOM_SEGMENTS(a.route_geometry,
b.route_geometry, 0.005)
FROM lrs_routes a, lrs_routes b
WHERE a.route_id = 11 AND b.route_id = 12;
-- Is the Route1 segment valid?
SELECT SDO_LRS.VALID_GEOM_SEGMENT(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- Is 50 a valid measure on Route1? (Should return FALSE; highest Route1 measure is 27.)
SELECT SDO_LRS.VALID_MEASURE(route_geometry, 50)
FROM lrs_routes WHERE route_id = 1;
-- Is the Route1 segment defined?
SELECT SDO_LRS.IS_GEOM_SEGMENT_DEFINED(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- How long is Route1?
SELECT SDO_LRS.GEOM_SEGMENT_LENGTH(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- What is the start measure of Route1?
SELECT SDO_LRS.GEOM_SEGMENT_START_MEASURE(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- What is the end measure of Route1?
SELECT SDO_LRS.GEOM_SEGMENT_END_MEASURE(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- What is the start point of Route1?
SELECT SDO_LRS.GEOM_SEGMENT_START_PT(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- What is the end point of Route1?
SELECT SDO_LRS.GEOM_SEGMENT_END_PT(route_geometry)
FROM lrs_routes WHERE route_id = 1;
-- Translate (shift measure values) (+10).
-- First, display the original segment; then, translate.
SELECT a.route_geometry FROM lrs_routes a WHERE a.route_id = 1;
SELECT SDO_LRS.TRANSLATE_MEASURE(a.route_geometry, m.diminfo, 10)
FROM lrs_routes a, user_sdo_geom_metadata m
WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
AND a.route_id = 1;
-- Redefine geometric segment to "convert" miles to kilometers
DECLARE
geom_segment SDO_GEOMETRY;
dim_array SDO_DIM_ARRAY;
BEGIN
SELECT a.route_geometry into geom_segment FROM lrs_routes a
WHERE a.route_name = 'Route1';
SELECT m.diminfo into dim_array from
user_sdo_geom_metadata m
WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY';
-- "Convert" mile measures to kilometers (27 * 1.609 = 43.443).
SDO_LRS.REDEFINE_GEOM_SEGMENT (geom_segment,
dim_array,
0, -- Zero starting measure: LRS segment starts at start of route.
43.443); -- End of LRS segment. 27 miles = 43.443 kilometers.
-- Update and insert geometries into table, to display later.
UPDATE lrs_routes a SET a.route_geometry = geom_segment
WHERE a.route_id = 1;
END;/
-- Display the redefined segment, with all measures "converted."
SELECT a.route_geometry FROM lrs_routes a WHERE a.route_id = 1;
-- Clip a piece of Route1.
SELECT SDO_LRS.CLIP_GEOM_SEGMENT(route_geometry, 5, 10)
FROM lrs_routes WHERE route_id = 1;
-- Point (9,3,NULL) is off the road; should return (9,4,9).
SELECT SDO_LRS.PROJECT_PT(route_geometry,
SDO_GEOMETRY(3301, NULL, NULL,
SDO_ELEM_INFO_ARRAY(1, 1, 1),
SDO_ORDINATE_ARRAY(9, 3, NULL)) )
FROM lrs_routes WHERE route_id = 1;
-- Return the measure of the projected point.
SELECT SDO_LRS.GET_MEASURE(
SDO_LRS.PROJECT_PT(a.route_geometry, m.diminfo,
SDO_GEOMETRY(3301, NULL, NULL,
SDO_ELEM_INFO_ARRAY(1, 1, 1),
SDO_ORDINATE_ARRAY(9, 3, NULL)) ),
m.diminfo )
FROM lrs_routes a, user_sdo_geom_metadata m
WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
AND a.route_id = 1;
-- Is point (9,3,NULL) a valid LRS point? (Should return TRUE.)
SELECT SDO_LRS.VALID_LRS_PT(
SDO_GEOMETRY(3301, NULL, NULL,
SDO_ELEM_INFO_ARRAY(1, 1, 1),
SDO_ORDINATE_ARRAY(9, 3, NULL)),
m.diminfo)
FROM lrs_routes a, user_sdo_geom_metadata m
WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
AND a.route_id = 1;
-- Locate the point on Route1 at measure 9, offset 0.
SELECT SDO_LRS.LOCATE_PT(route_geometry, 9, 0)
FROM lrs_routes WHERE route_id = 1;
Example 7-3 shows the output of the SELECT statements in Example 7-2.
Example 7-3 Simplified Example: Output of SELECT Statements
SQL> -- First, display the data in the LRS table.
SQL> SELECT route_id, route_name, route_geometry FROM lrs_routes;
ROUTE_ID ROUTE_NAME
---------- --------------------------------
ROUTE_GEOMETRY(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y, Z), SDO_ELEM_INFO, SDO_ORDIN
--------------------------------------------------------------------------------
1 Route1
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 0, 2, 4, 2, 8, 4, 8, 12, 4, 12, 12, 10, 18, 8, 10, 22, 5, 14, 27))
11 result_geom_1
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 0, 2, 4, 2, 5, 4, 5))
12 result_geom_2
ROUTE_ID ROUTE_NAME
---------- --------------------------------
ROUTE_GEOMETRY(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y, Z), SDO_ELEM_INFO, SDO_ORDIN
--------------------------------------------------------------------------------
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
5, 4, 5, 8, 4, 8, 12, 4, 12, 12, 10, 18, 8, 10, 22, 5, 14, 27))
13 result_geom_3
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 0, 2, 4, 2, 5, 4, 5, 8, 4, 8, 12, 4, 12, 12, 10, 18, 8, 10, 22, 5, 14, 27)
)
SQL> -- Are result_geom_1 and result_geom2 connected?
SQL> SELECT SDO_LRS.CONNECTED_GEOM_SEGMENTS(a.route_geometry,
2 b.route_geometry, 0.005)
3 FROM lrs_routes a, lrs_routes b
4 WHERE a.route_id = 11 AND b.route_id = 12;
SDO_LRS.CONNECTED_GEOM_SEGMENTS(A.ROUTE_GEOMETRY,B.ROUTE_GEOMETRY,0.005)
--------------------------------------------------------------------------------
TRUE
SQL> -- Is the Route1 segment valid?
SQL> SELECT SDO_LRS.VALID_GEOM_SEGMENT(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.VALID_GEOM_SEGMENT(ROUTE_GEOMETRY)
--------------------------------------------------------------------------------
TRUE
SQL> -- Is 50 a valid measure on Route1? (Should return FALSE; highest Route1 measure is 27.)
SQL> SELECT SDO_LRS.VALID_MEASURE(route_geometry, 50)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.VALID_MEASURE(ROUTE_GEOMETRY,50)
--------------------------------------------------------------------------------
FALSE
SQL> -- Is the Route1 segment defined?
SQL> SELECT SDO_LRS.IS_GEOM_SEGMENT_DEFINED(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.IS_GEOM_SEGMENT_DEFINED(ROUTE_GEOMETRY)
--------------------------------------------------------------------------------
TRUE
SQL> -- How long is Route1?
SQL> SELECT SDO_LRS.GEOM_SEGMENT_LENGTH(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.GEOM_SEGMENT_LENGTH(ROUTE_GEOMETRY)
-------------------------------------------
27
SQL> -- What is the start measure of Route1?
SQL> SELECT SDO_LRS.GEOM_SEGMENT_START_MEASURE(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.GEOM_SEGMENT_START_MEASURE(ROUTE_GEOMETRY)
--------------------------------------------------
0
SQL> -- What is the end measure of Route1?
SQL> SELECT SDO_LRS.GEOM_SEGMENT_END_MEASURE(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.GEOM_SEGMENT_END_MEASURE(ROUTE_GEOMETRY)
------------------------------------------------
27
SQL> -- What is the start point of Route1?
SQL> SELECT SDO_LRS.GEOM_SEGMENT_START_PT(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.GEOM_SEGMENT_START_PT(ROUTE_GEOMETRY)(SDO_GTYPE, SDO_SRID, SDO_POINT(X,
--------------------------------------------------------------------------------
SDO_GEOMETRY(3301, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 1, 1), SDO_ORDINATE_ARRAY(
2, 2, 0))
SQL> -- What is the end point of Route1?
SQL> SELECT SDO_LRS.GEOM_SEGMENT_END_PT(route_geometry)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.GEOM_SEGMENT_END_PT(ROUTE_GEOMETRY)(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y,
--------------------------------------------------------------------------------
SDO_GEOMETRY(3301, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 1, 1), SDO_ORDINATE_ARRAY(
5, 14, 27))
SQL> -- Translate (shift measure values) (+10).
SQL> -- First, display the original segment; then, translate.
SQL> SELECT a.route_geometry FROM lrs_routes a WHERE a.route_id = 1;
ROUTE_GEOMETRY(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y, Z), SDO_ELEM_INFO, SDO_ORDIN
--------------------------------------------------------------------------------
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 0, 2, 4, 2, 8, 4, 8, 12, 4, 12, 12, 10, 18, 8, 10, 22, 5, 14, 27))
SQL> SELECT SDO_LRS.TRANSLATE_MEASURE(a.route_geometry, m.diminfo, 10)
2 FROM lrs_routes a, user_sdo_geom_metadata m
3 WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
4 AND a.route_id = 1;
SDO_LRS.TRANSLATE_MEASURE(A.ROUTE_GEOMETRY,M.DIMINFO,10)(SDO_GTYPE, SDO_SRID, SD
--------------------------------------------------------------------------------
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 10, 2, 4, 12, 8, 4, 18, 12, 4, 22, 12, 10, 28, 8, 10, 32, 5, 14, 37))
SQL> -- Redefine geometric segment to "convert" miles to kilometers
SQL> DECLARE
2 geom_segment SDO_GEOMETRY;
3 dim_array SDO_DIM_ARRAY;
4
5 BEGIN
6
7 SELECT a.route_geometry into geom_segment FROM lrs_routes a
8 WHERE a.route_name = 'Route1';
9 SELECT m.diminfo into dim_array from
10 user_sdo_geom_metadata m
11 WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY';
12
13 -- "Convert" mile measures to kilometers (27 * 1.609 = 43.443).
14 SDO_LRS.REDEFINE_GEOM_SEGMENT (geom_segment,
15 dim_array,
16 0, -- Zero starting measure: LRS segment starts at start of route.
17 43.443); -- End of LRS segment. 27 miles = 43.443 kilometers.
18
19 -- Update and insert geometries into table, to display later.
20 UPDATE lrs_routes a SET a.route_geometry = geom_segment
21 WHERE a.route_id = 1;
22
23 END;
24 /
PL/SQL procedure successfully completed.
SQL> -- Display the redefined segment, with all measures "converted."
SQL> SELECT a.route_geometry FROM lrs_routes a WHERE a.route_id = 1;
ROUTE_GEOMETRY(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y, Z), SDO_ELEM_INFO, SDO_ORDIN
--------------------------------------------------------------------------------
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
2, 2, 0, 2, 4, 3.218, 8, 4, 12.872, 12, 4, 19.308, 12, 10, 28.962, 8, 10, 35.398
, 5, 14, 43.443))
SQL> -- Clip a piece of Route1.
SQL> SELECT SDO_LRS.CLIP_GEOM_SEGMENT(route_geometry, 5, 10)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.CLIP_GEOM_SEGMENT(ROUTE_GEOMETRY,5,10)(SDO_GTYPE, SDO_SRID, SDO_POINT(X,
--------------------------------------------------------------------------------
SDO_GEOMETRY(3302, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 2, 1), SDO_ORDINATE_ARRAY(
5, 4, 5, 8, 4, 8, 10, 4, 10))
SQL> -- Point (9,3,NULL) is off the road; should return (9,4,9).
SQL> SELECT SDO_LRS.PROJECT_PT(route_geometry,
2 SDO_GEOMETRY(3301, NULL, NULL,
3 SDO_ELEM_INFO_ARRAY(1, 1, 1),
4 SDO_ORDINATE_ARRAY(9, 3, NULL)) )
5 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.PROJECT_PT(ROUTE_GEOMETRY,SDO_GEOMETRY(3301,NULL,NULL,SDO_EL
--------------------------------------------------------------------------------
SDO_GEOMETRY(3301, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 1, 1), SDO_ORDINATE_ARRAY(
9, 4, 9))
SQL> -- Return the measure of the projected point.
SQL> SELECT SDO_LRS.GET_MEASURE(
2 SDO_LRS.PROJECT_PT(a.route_geometry, m.diminfo,
3 SDO_GEOMETRY(3301, NULL, NULL,
4 SDO_ELEM_INFO_ARRAY(1, 1, 1),
5 SDO_ORDINATE_ARRAY(9, 3, NULL)) ),
6 m.diminfo )
7 FROM lrs_routes a, user_sdo_geom_metadata m
8 WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
9 AND a.route_id = 1;
SDO_LRS.GET_MEASURE(SDO_LRS.PROJECT_PT(A.ROUTE_GEOMETRY,M.DIMINFO,SDO_GEOM
--------------------------------------------------------------------------------
9
SQL> -- Is point (9,3,NULL) a valid LRS point? (Should return TRUE.)
SQL> SELECT SDO_LRS.VALID_LRS_PT(
2 SDO_GEOMETRY(3301, NULL, NULL,
3 SDO_ELEM_INFO_ARRAY(1, 1, 1),
4 SDO_ORDINATE_ARRAY(9, 3, NULL)),
5 m.diminfo)
6 FROM lrs_routes a, user_sdo_geom_metadata m
7 WHERE m.table_name = 'LRS_ROUTES' AND m.column_name = 'ROUTE_GEOMETRY'
8 AND a.route_id = 1;
SDO_LRS.VALID_LRS_PT(SDO_GEOMETRY(3301,NULL,NULL,SDO_ELEM_INFO_ARRAY
------------------------------------------------------------------------------
TRUE
SQL> -- Locate the point on Route1 at measure 9, offset 0.
SQL> SELECT SDO_LRS.LOCATE_PT(route_geometry, 9, 0)
2 FROM lrs_routes WHERE route_id = 1;
SDO_LRS.LOCATE_PT(ROUTE_GEOMETRY,9,0)(SDO_GTYPE, SDO_SRID, SDO_POINT(X, Y, Z), S
--------------------------------------------------------------------------------
SDO_GEOMETRY(3301, NULL, NULL, SDO_ELEM_INFO_ARRAY(1, 1, 1), SDO_ORDINATE_ARRAY(
9, 4, 9))